고정 헤더 영역
상세 컨텐츠
본문
1. Descrete CASE, PMF 변환
예를들어 $$B (4,{1\over{2}} )$$의 이항분포가 있다고하자
그리고 $$ Y= {1\over{X+1}}$$ 인 Y로 변환한다고하면
아래와 같이 변환된다
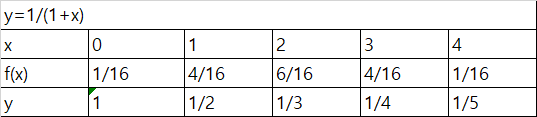
2. Continuous Case, PDF 변환
$$Y=u(X)$$라는 transform 함수는 monotone increase(decrease)임을 가정한다
이때 역함수는 $$X=u^{-1}(Y)=w(Y)$$
원래의 확률 밀도함수가 $$f(x)$$이면,
변환된 확률 함수는
$$|w'(Y)|f(w(Y))$$가 된다
예제)

$$Y=-lnX$$는 단조 감소함수고,
$$w(Y)=e^{-Y}$$다.
$$f(x) = 1 when 0<x<1$$인 uniform distribution
따라서 변환함수 $$g(y)= |-e^{-y} |* f( e^{-y}) = e^{-y} $$
2-1 log normal distribution
log normal distribution은 정규분포함수에 $$ Y= e^X $$ transform 한것이다
즉, $$lnY=X$$가된다.
정규분포의 확률밀도함수 $$f(x) = {1\over{\sigma \sqrt{2\pi} }} exp( {-(X-\mu)^2\over{2\sigma^2 }} )$$고
$$ w'(Y)= {dx\over{dy}}= {1\over{y}} $$
따라서 변환식 $$g(y) = {1\over{y\sigma \sqrt{2\pi} }} exp( {-(lny-\mu)^2\over{2\sigma^2 }} ) $$ $$ when y>0 $$
$$ E(Y) = e^{\mu + {\sigma^2 \over{2}}}$$ 가 성립한다.
'코딩일기장 > 통계학' 카테고리의 다른 글
| (n-1)s^2/sigma^2 (0) | 2021.11.29 |
|---|---|
| 자기회귀모형 Auto Regression (0) | 2021.10.25 |
| Moment와 Moment generating function (0) | 2021.10.05 |
| Jensen Inequality (0) | 2021.10.05 |
| Markov Inequality, Chebyshev Inequality (0) | 2021.10.05 |





댓글 영역